Как я планету в Unity генерировал, часть вторая

Это третья часть истории о том, как разрабатывалась игра «Rocket Science», и продолжение рассказа о генерации планеты средствами Юнити.

Земля в Space Engine выгдядит великолепно

Однажды Бертран Мейер поделился идеей книги об объектно-ориентированном конструировании программных систем со своим другом. На что тот ответил, что каждая строка программного кода в ней уменьшит количество читателей вдвое. Однако это не помешало Бертрану вставлять куски кода на каждую страницу книги, и при этом она стала библией объектно-ориентированного проектирования. Я же не смогу позволить себе такую роскошь и поэтому расскажу о разработке системы генерации планеты через описание принятых решений, возникающих в связи с этим проблем и полученных результатов. Однако базовые знания программирования, линейной алгебры и Юнити очень помогут в восприятии написанного материала.

За три года в геймдеве я вывел для себя способ эффективной работы и борьбы с прокрастинацией. Когда ты работаешь один, ты не можешь позволить себе несколько месяцев разрабатывать прототип, потом полностью выбрасывать его и писать игру с чистого листа, но «нормально» — быстро закончится запал, да и кушать тоже что-то нужно. Но и полностью спроектировать все системы игры, как это делается в энтерпрайзе, тоже никогда не получится, потому что концепции, механики и идеи постоянно меняются по ходу разработки. За примером не надо далеко идти — Илон тоже начинался как простенький клон Into Space 2, а сейчас я сижу и генерирую планеты и подумываю об орбитальных механиках. Поэтому для меня лучшим вариантом стал «прототипо-итерируемый» подход. При разработке новой игровой системы необходимо максимально быстро добиться видимого результата на экране, после чего итерациями добавлять фичи и исправлять баги до тех пор, пока система не наберет критическую массу некачественного кода, когда любое изменение порождает больше проблем, чем добавляет возможностей. После чего выделяется время на рефакторинг и мини-проектирование, когда к постоянно меняющимся и расширяющимся частям применяются подходы ООП и шаблоны проектирования. И далее процесс повторяется.

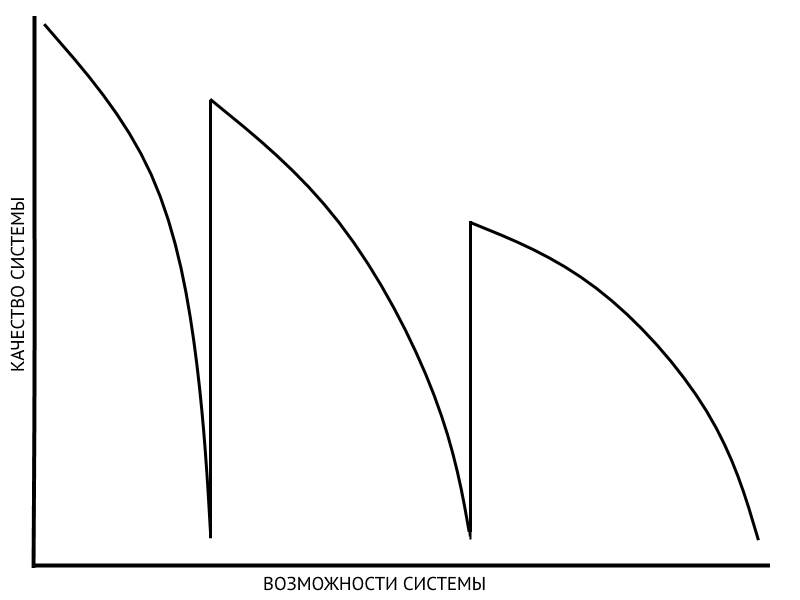Вертикальные скачки иллюстрируют собой результаты рефакторинга. Но чтобы вы ни делали, рано или поздно ваша система скорее всего скатится

С чего же начать при создании системы генерации планеты? Для моего случая, когда я хотел запускать ракету с поверхности и плавно переходить в космос, лучшим решением из тех, что я видел на этапе исследования, оказалась сфера, состоящая из квадродеревьев. Звучит страшно, но если разбить задачу на небольшие итерации, то всё оказывается гораздо проще. Похоже, настало время применить описанный выше подход.

Последние приготовления

Для начала мне нужно было сгенерировать единичный куб, состоящий из шести квадрантов. Проще говоря куб, состоящий из шести плоскостей, расстояние от центра которого до каждой стороны равно одной единице. В Юнити эта единица равна одному метру, поэтому дальше я буду все измерять в метрах.

Я создал плоскость в Синеме, размером 2x2 метра, состоящую из 16x16 полигонов, закинул в Юнити и в настройках импорта включил возможность чтения/записи. Теперь у меня был доступ к массиву вершин и массиву треугольников, и можно было делать с ними все, что душа пожелает.

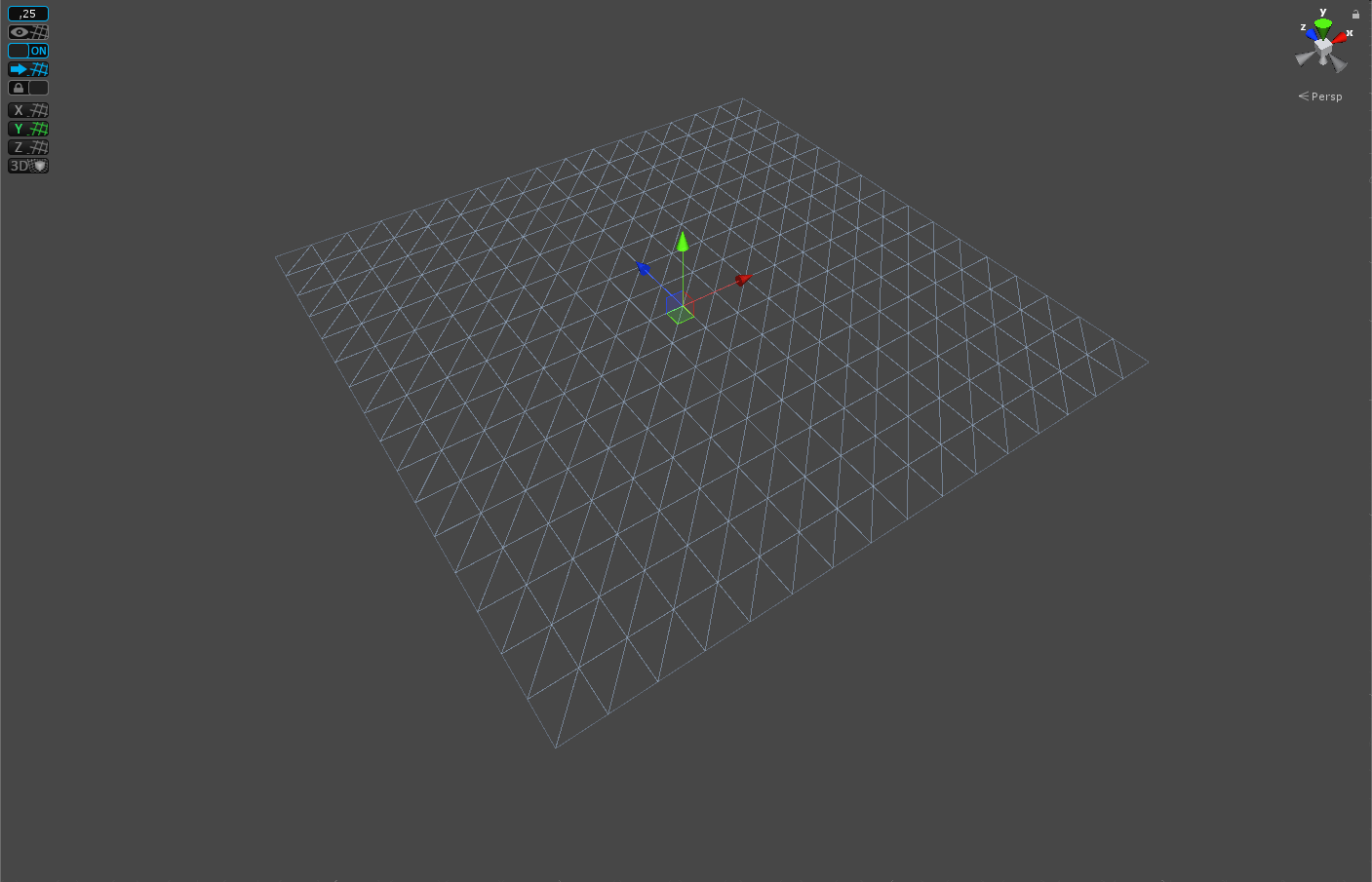Kerbal Space Program использует 10x10 полигонов. Space Engine 32x32. Я решил остановиться где-то посередине

Теперь, чтобы создать, например, сторону куба, которая будет располагаться в позиции (0, 0, -1), необходимо сдвинуть каждую вершину исходной плоскости на этот вектор и повернуть на (270, 0, 0). Те, кто познал силу матриц, уже поняли, что это можно сделать обычной TR матрицей, остальные же смогут обойтись векторными операциями. Полученный массив вершин вместе с исходными треугольниками плоскости запихиваются в новый меш на сцене и сторона готова. Я проделал этот трюк с пятью оставшимися сторонами, смещая, вращая и запихивая вершины, и получил закономерный результат.

Единичный куб

Чтобы получить из куба единичную сферу, нужно лишь после смещения и поворота вершины ее нормализовать.

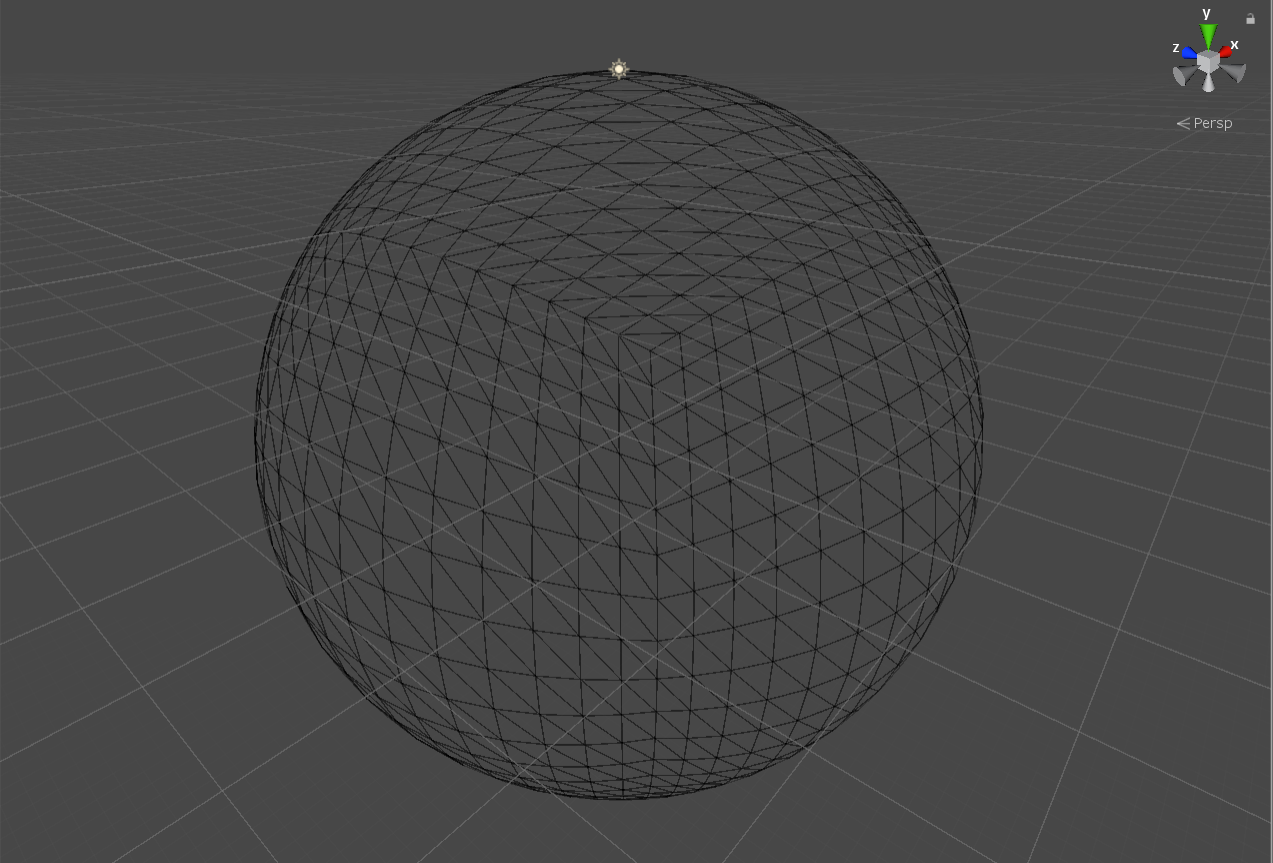По сравнению с обычной сферой в Юнити, здесь искажения сосредоточены не у полюсов, а распределены на стыках между сторонами

Эта сфера состоит из 16 * 16 * 6 = 1536 полигонов. Что для планеты размером с Землю маловато. Но суть выбранного способа заключается в том, что каждую сторону (давайте далее называть ее квадрантом) этой кубосферы можно разбить на четыре, проделав примерно тот же набор операций, что и раньше. И число полигонов станет равным 16 * 16 * 6 * 4 = 6144. Это называется повышением уровня разбиения сферы, и если предыдущая сфера была нулевого уровня, то новая будет первого. Операцию можно повторять, рекурсивно разбивая квадранты, при этом есть простая формула, которая будет описывать зависимость количества полигонов сферы от ее уровня разбиения:

полигоны = 256 * 6 * 4 ^ уровень

То есть на 10 уровне количество полигонов будет равно 1 610 612 736, что уже неплохо. Я не стал забивать себе голову вопросами о том, как это всё отрендерить в Юнити, и занялся реализацией разбиения.

Основа основ

Мне нужна была структура данных, описывающая свойства квадранта, которая позволила бы вычислять данные потомков во время разбиения из данных их предка. Для этого подходило квадродерево (логично было предположить из названия метода), где каждый элемент хранит следующий набор данных:

• уникальный идентификатор (или индекс) квадранта;
• уровень разбиения;

четыре идентификатора потомков;

• идентификатор предка;
• позиция;
• поворот.

Здесь я решил использовать не объекты, а структуры, так как чувствовал что в будущем придется много итерироваться по возможно большим массивам квадрантов. В отличие от объектов, которые разбросаны в оперативной памяти случайным образом, структуры в массивах будут располагаться в едином последовательном блоке памяти, и процессор будет обрабатывать их быстрее за счет кеширования.

К примеру, данные многострадального квадранта, с которого я начал свои эксперименты будет выглядеть следующим образом (не обращайте пока внимания на индекс, о нем я расскажу позже).

Quad 
index: 23 
level: 0 
childrenIds: 0 0 0 0 
parentId: 0 
position: (0, 0, -1) 
rotation: (270, 0, 0)

На данный момент структура пестрит нулями, но все изменится во время операции разбиения. Что происходит в этот момент? Ответ даст очередная серая картинка:

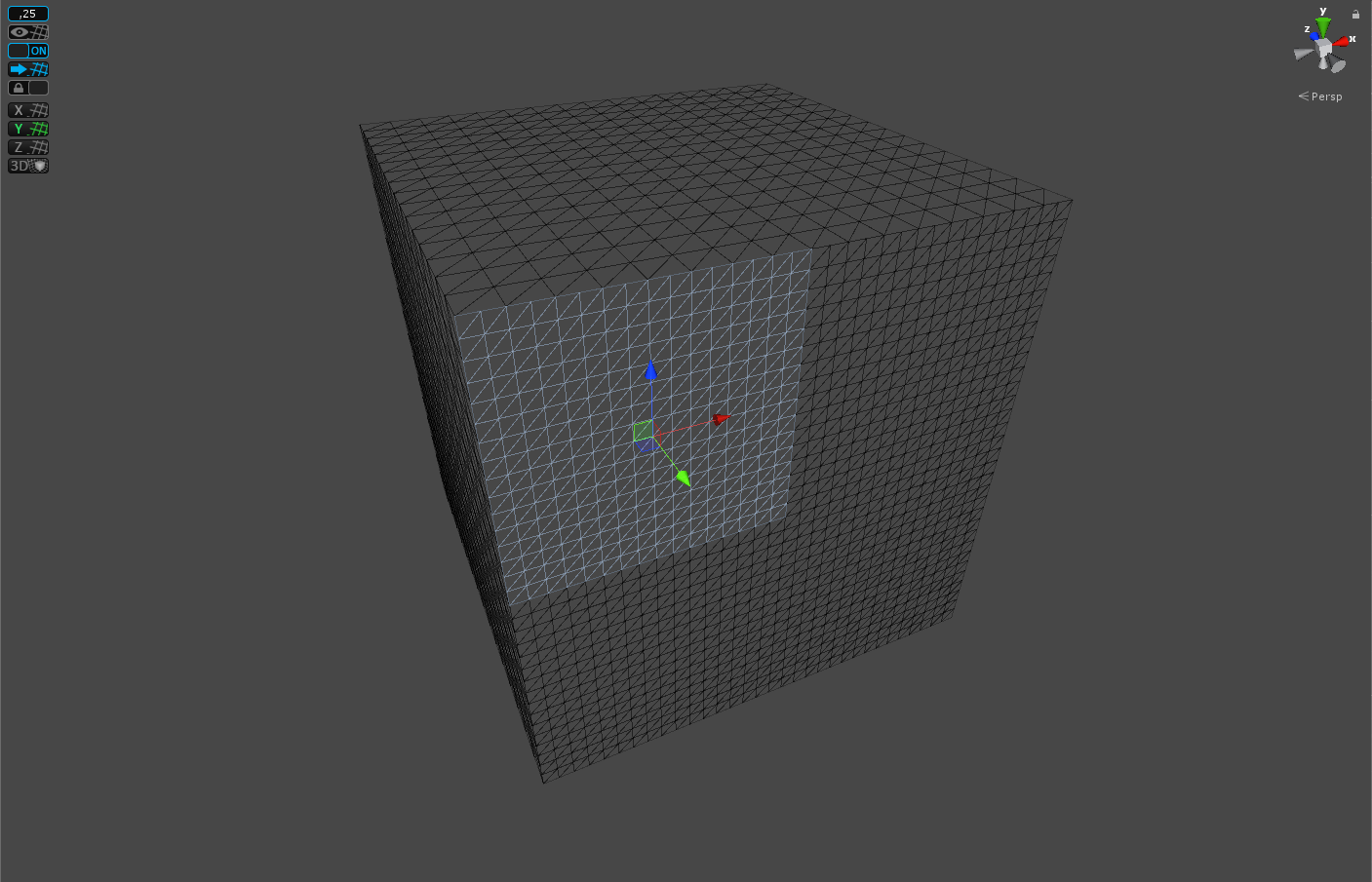При производстве этого изображения ни один куб не пострадал

Мы должны создать четыре потомка, каждый из которых должен быть смещен относительно позиции своего предка и уменьшен в 2 раза. Также для каждого потомка нужно записать индекс предка и увеличить уровень разбиения на 1, а для предка записать индексы потомков. Таким образом данные оригинально квадранта станут такими:

Quad 
index: 23 
level: 0 
childrenIds: 123 223 323 423 
parentId: 0 
position: (0, 0, -1) 
rotation: (270, 0, 0)

А выделенного на изображении потомка:

Quad 
index: 123 
level: 1 
childrenIds: 0 0 0 0 
parentId: 23 
position: (-0.5, 0.5, -1) 
rotation: (270, 0, 0)

Заметьте, что поворот у потомка никак не изменился. В будущем можно будет вычислять поворот из корневого предка и убрать его из структуры, но пока пусть остается для удобства. Еще среди этих данных нет информации о скейле квадранта. Но его легко вычислить исходя из уровня разбиения:

скейл = 1 / (2 ^ уровень)

Теперь, как говорили мои преподаватели в университете, становится очевидно, как из этих данных сгенерировать сферу с уровнем разбиения 1. Для начала я вынес весь ранее написанный код, работающий с вершинами, треугольниками и мешами, в отдельный класс который назвал QuadBuilder. На вход он будет получать Quad с готовыми данными и генерировать из них меш. В этот класс после поворота, но до нормализации я добавил операцию Scale, которая будет менять размер квадранта в зависимости от его уровня разбиения.

Следующий недостающий ингредиент — класс, который будет хранить квадранты и уметь создавать и разбивать их. Его я назвал QuadBody, а в качестве контейнера для квадрантов выбрал список (List), так как количество квадрантов, которые мне понадобятся, заранее неизвестно. И теперь весь алгоритм генерации стал выглядеть следующим образом.

• Создаем QuadBody.
• Вызываем метод CreateRootQuads(), который создаст шесть базовых квадрантов из начала статьи и положит их в список.

Вызываем метод SplitAll(), где для каждого базового квадранта будут созданы по четыре потомка и тоже размещены в списке.

Передаем список квадрантов в QuadBuilder, где для каждого элемента списка он сгенерирует меш и поставит его на сцену. При этом, если у квадранта есть потомки, то меш нужно скрыть, так как он не нужен.

• Profit.

Нужно больше полигонов

К этому моменту мне надоело смотреть на сгенерированную полигональную сетку, поэтому я решил привнести на сцену немного цвета. Для визуализации меша помимо материала, нужны еще нормали для каждой вершины. Для тех, кто не знает, что это такое, есть отличное видео на Ютубе, которое раз и навсегда поставит точку в этом вопросе. Их можно рассчитать самостоятельно, но в Юнити есть метод у меша, называемый RecalculateNormals(), который все сделает за вас. Это в совокупности с обычным белым материалом привело к следующему результату.

Сфера во всей ее красоте

Выглядело в целом неплохо, однако были хорошо различимы стыки квадрантов. Это все потому, что Юнити при расчете нормалей для каждого квадранта ничего не знает о соседних и поэтому не может их учесть в своих вычислениях. Поэтому нормали придется считать все-таки вручную. Я решил эту проблему отложить и заняться более приоритетной на тот момент задачей.

Чисто теоретически, можно было вызвать SplitAll() столько раз, сколько уровней разбиения мне было нужно, но после 5 уровня Юнити сильно задумалось, на восьмом-девятом молча закрылось, а на одиннадцатом еще и удалилось с компьютера. Это было ожидаемо, так как не каждый движок сможет отрендерить сотни миллионов полигонов, и это стало следующей задачей, которую мне предстояло решить.

Добрые соседи

Пока я работал с единичной сферой, я видел большую ее часть. Но все должно было измениться в момент её превращения в полноценную планету. Чтобы понять, что же изменится, я решил сделать «планету» радиусом в 100 метров. Все что было нужно сделать, это вершину после нормализации в QuadBuilder умножить на радиус. И в этом заключается прелесть единичной сферы, что ее вершины встанут в нужное место с помощью такой простой операции. При этом вид из камеры получился волшебный.

Похожую кривизну горизонта можно наблюдать в другой игре о космосе — Astroneer

Мы видим небольшую часть планеты в каждый момент времени, а значит разбивать квадранты, которые не видны, не нужно. Кроме того, чем дальше квадрант находится от камеры, тем меньший уровень разбиения ему нужен. И когда квадрант пропадет из области видимости или камера от него отдалится, не имеет смысла держать его в разбитом состоянии, тратя драгоценные ресурсы компьютера, а значит необходимо комбинировать его потомков. Это так называемый Quadtree Level Of Detail (QLOD). Чтобы его реализовать нужно добавить два новых метода в QuadBody: Split(index) и Combine(index), где index — это индексы квадрантов, которые нужно разбить или объединить.

Операция объединения гораздо проще разбиения. Все что нужно сделать, это пройтись по childrenIds, удалить из списка соответствующие квадранты и обнулить childrenIds. Однако здесь возникает вопрос, каким образом искать квадранты по индексу в списке. Линейный поиск не очень подойдет, так как по сути при каждой операции комбинирования придется четыре раза пройтись по всему списку. Сортировать список, чтобы воспользоваться бинарным поиском, тоже будет дорого, так как операция разбиения будет вызываться достаточно часто.

Здесь я решил пожертвовать памятью в угоду производительности. Я создал словарь (Dictionary), ключами которого были индексы квадрантов, а значениями — их позиции в списке. При добавлении нового квадранта в список просто добавляем в словарь его индекс и позицию — она всегда будет последней. Для удаления необходимо получить позицию квадранта в словаре, и удалить его из списка и словаря. Здесь можно сразу реализовать еще одну простую оптимизацию. Если квадрант будет находиться в середине списка, то после удаления C # должен будет сдвинуть все элементы, стоящие после него на одну позицию назад, чтобы в списке не было разрывов. Чтобы избежать этого нужно поменять местами удаляемый элемент и последний (не забыв обновить их позиции в словаре) и тогда операция удаления пройдет гладко и красиво.

Моя неловкая попытка проиллюстрировать предыдущий абзас

Формально, метод SplitAll() больше не нужен, так как теперь можно разбивать только нужные квадранты. Для эксперимента я выставил сфере радиус 5 и решил разбить только один квадрант на один уровень.

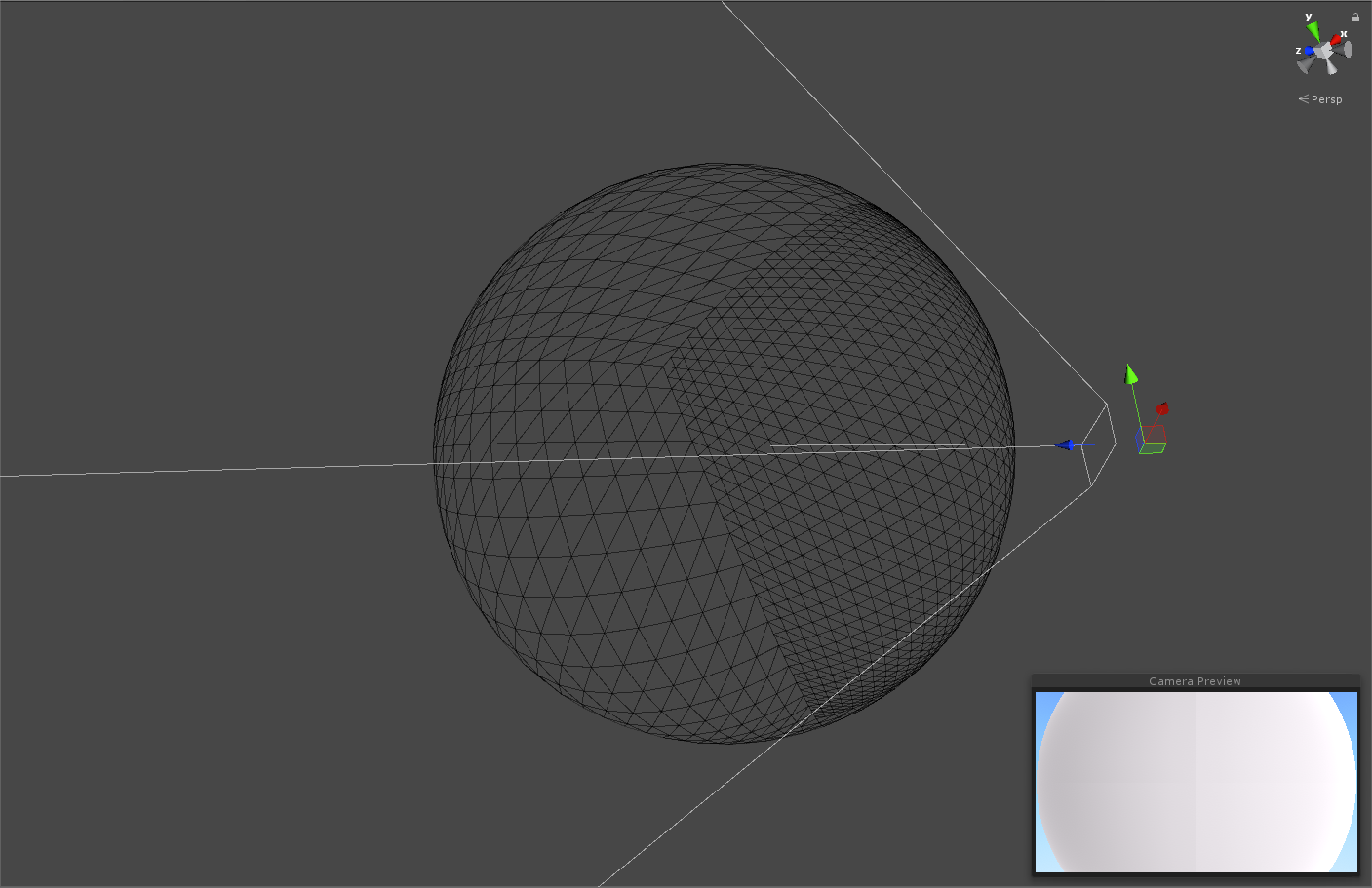Увеличенная детализация поверхности у камеры

Выглядит как ровно то, что нужно, однако следующая проблема не заставила себя ждать. На границе уровней возникали «повисшие в воздухе вершины», которые в режиме сферы не доставляют неудобств, но как только к планете будет применена карта высот, то в этих местах возникнут разрывы.

Примеры разрывов

Я решил сделать перерыв, приготовил себе салат из мха и лишайника и стал размышлять и пройденном пути. Я решал одну проблему, а на ее месте возникало четыре других и, казалось, что этому не будет конца. Может стоило все бросить и вернуться к клонированию Into Space 2? Но, черт побери, это было вызовом. Ты либо принимаешь его, идешь до конца, решаешь все проблемы, делаешь красивые, работающие системы, потом релизишь игру и ее никто не покупает, после чего устраиваешься на работу двигать баннеры на один пиксель до конца жизни. Либо сразу сдаешься и идешь двигать баннеры. Так как обе дороги приводят в одну точку, то я решил продолжить двигаться по длинному, но интересному пути.

Решение у этой задачи одновременно и простое, и сложное. Простота заключается в том, что нам нужно, чтобы между двумя квадрантами была разница максимум в 1 уровень разбиения. И на стыке между большим уровнем разбиения и меньшим, нужно использовать не стандартный массив треугольников, а модифицированный, который пропускал бы часть вершин.

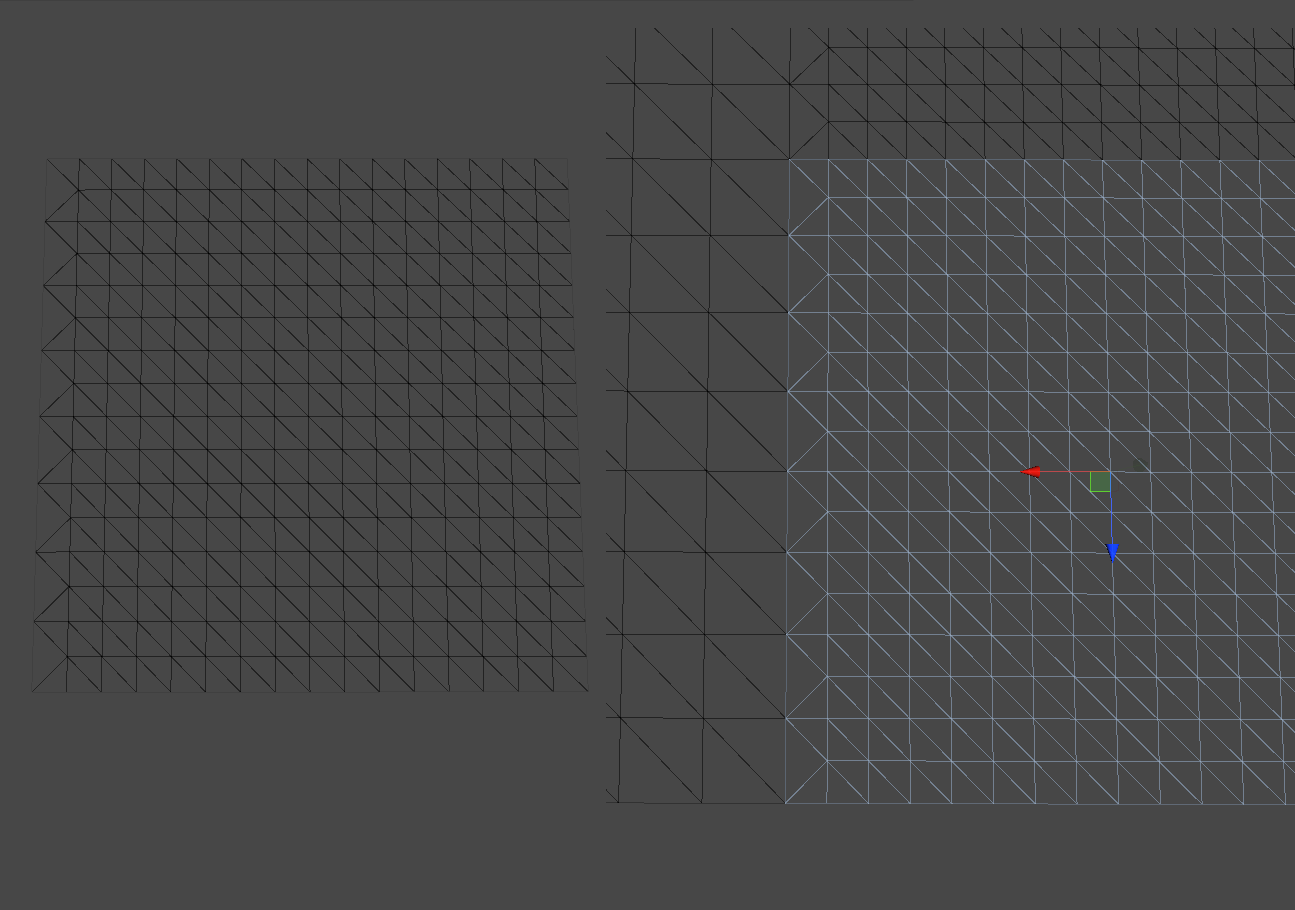Слева квадрант, у которого вдоль всей левой стороны пропущены вершины, а справа вид на стык с квадрантом меньшего уровня разбиения

Сложность заключается в том, что всего существует 16 разных вариантов того, где могут находиться эти стыки — от случая, изображенного на картинке, до варианта, когда пропуски должны быть сделаны на всех границах квадранта. И наверное единственный эффективный способ все эти случаи обрабатывать — это рассчитать все варианты треугольников заранее, закешировать их и выбирать нужные в зависимости от состояния соседей квадранта, которых теперь тоже нужно знать, что выливается в отдельную проблему.

Я решил начать с поиска соседей квадранта и, к счастью, достаточно быстро вышел на научную работу, которая называется A Practical Algorithm for Computing Neighbors in Quadtrees, Octrees, and Hyperoctrees. В ней был предложен, элегантный и производительный способ, как это можно сделать. Все что нужно, это задавать индексы квадрантам определенным образом, который отлично иллюстрирует следующее изображение.

Это проще, чем кажется на первый взгляд

После чего строится таблица, с помощью которой, зная индекс квадранта и направление соседа, индекс соседа и рассчитывается. Я не буду приводить здесь этот алгоритм, тем, кому интересно, рекомендую почитать работу. Что дает нам знание индексов соседей? Возможность в любой момент проверить есть ли у QuadBody квадранты с такими индексами. Если их нет, значит сосед еще не был разбит и нужно применять треугольники с пропусками.

С генерацией треугольников с пропусками вершин все было интересней. Вначале я решил сделать их в Синеме, но обнаружилось, что либо в Синеме при объединении двух треугольников меняются индексы вершин, либо Юнити не очень любит пропущенные вершины и что-то там меняет, в итоге, когда я применял треугольники одного меша на вершинах другого, всё превращалось в жуткое месиво. И так как я не смог быстро придумать алгоритм, рассчитывающий пропуски, и он должен был отработать всего один раз, я решил посчитать треугольники вручную. Это вылилось в двухдневный ад, который даже нет сил описывать. Однако в итоге я и с этим разобрался. Далее осталось модифицировать алгоритм в двух местах.

Во-первых при разбиении квадрантов, мы должны рассчитать четырех возможных соседей и сохранить их в Quad. Таким образом там появляется еще одно поле, называемое neighborIds. Во вторых, после разбиения нужно лишь проверить, если ли соседи по таким индексам и применить соответствующий набор треугольников. И вуаля!

Идеальный переход между уровнями

Это была маленькая победа в тяжелой войне за процедурную генерацию планеты с адаптивным уровнем детализации. Но выиграть битву — не значит выиграть войну. Впереди меня ждало увлекательное приключение в мир планетарных масштабов, неудержимой оптимизации, переполненных интов и ошибок вычислений на флоатах, приправленных страданиями с uv и нормалями. Обо всем этом в следующей статье на DTF, если это все еще будет кому-то интересно.

По традиции оставляю страницу игры в Стиме и ссылки на каналы в Телеграме и Дискорде. До скорой встречи.